
(Windows11/10 WSL2版)

C++言語はB.ストラウストラップ(Bjarne Stroustrup)博士によって1980年代初頭に設計されたプログラム言語として有名です。C言語文法との上位交換性があり、抱負な機能が盛り込まれていることでも知られています。ここでは、そのすべてについて日本語を使ったC++言語の適用例を挙げることはとうていできません。従ってほんの一部ではありますが、今回のプログラミング言語で日本語多めにというテーマで、いくつかの実例を紹介してみたいと思います。
もちろんプログラム言語について何も知らない方が、いきなりC++言語を習得しようとしても大変難しいのではないかと思います。まずはC言語の流儀に、ある程度慣れてからC++言語に進むのがよいのではないでしょうか。 Windows11/10 WSL2版ではWindows11/10のコマンドプロンプトを起動させて、プログラムの作成、機械翻訳(コンパイル)、実行を行います。また、PowerShell上のC言語の処理系には今回もEmbarcadero Technologies社のC言語コンパイラー(bcc32c)をインストールして使用し、日本語多めの検証をしてみました。 この処理系は入力ファイルの拡張子が「.c」であれば、C言語として処理しますが、「.cpp」であれば自動的にC++言語として処理をしてくれます。
現在、Windows11/10上でLinux(Ubuntu)OSを動作させるWSL(Windwos Subsystem for Linux)という便利な仕組みが使えるようになっています。これによってUbuntu OS上の日本語カスタマイザーを使って、Windows11/10上の日本語C++言語を動かすことができます。
WSLのインストールについては、他のさまざまなサイトで紹介されていますので、そちらを参照してみてください。今回はWindwos11(バージョン23H2)上で、WSL2(Ubuntu22.04)をインストールして使っています。下図はPowerShellからWSLのバージョンを確認した様子です。(Window10もWSL2です)
WSL2を起動させてインストールしたFLEXのバージョン(V 2.6.4)を確認してみます。
WSLやPowerShellで動作するC++言語用の日本語カスタマイザーは、FLEXのプログラムを使います。それをC言語処理系によって翻訳することにより、プログラムを実行することができます。従って日本語カスタマイザーを動かすにはWSL上でFLEXとC++言語の処理系(gcc)が必要となります。以下に今回使用したWSL2上のgccバージョンを示します。
また、PowerShellで動作するclang準拠のC言語処理系、bcc32cのバージョン(フリー入手可能 V7.30)を以下に示します。
ここで、C言語編と同じように、日本語で書かれたC++言語ファイルの名前を仮にファイル1.jcppとすると
>jcpp ファイル1
というバッチコマンドによりファイル1.cppを生成し、さらに翻訳(コンパイル)、結合(リンク)して、実行可能形式ファイルであるファイル1を生成します。 PowerShell上のbcc32cで動作させるために、ファイル1.cのみ生成するには、「-c」オプションを付けるようにしています。 このとき、jcpp_rulew(C++と共用)がC++言語用の日本語カスタマイザー1パス目の実行で、jcpp_rulew2は2パス目の実行を行っています。 このとき、WSL用の日本語カスタマイザー「jcpp_rulew」では、読み込むテキストファイルの改行処理に、UbuntuのLF(\n)に加え、WindowsのCRLF(\r\n)でも認識できるようにしてあります。
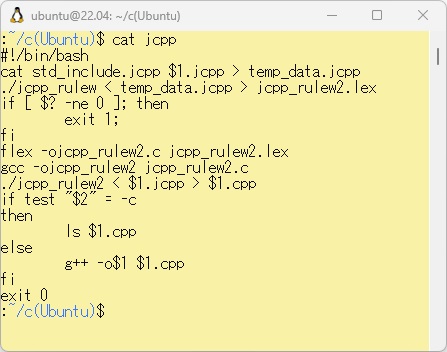
さらに翻訳(コンパイル)、結合(リンク)して、実行可能形式ファイルであるファイル1.exeを生成します。jcppという日本語カスタマイザー実行プログラムはC言語の場合とほとんど同じ仕様ですが、C++言語での処理系は、「g++」で実行します。
ここで、日本語定義の領域がかなり大きくなってきましたので、C++言語編からは自分でよく使う予約語や演算子などの日本語定義部分をプログラムとは別に、「std_include10.jcpp」として外部である程度まとめて宣言できるようにしておきます。 そして処理するときにバッチコマンドの機能を利用し、宣言ファイルと日本語C++ファイルを結合します。このように日本語定義部分を通常のC++言語の文法に合うように置き換えるという処理をします。
以下は、別に定義した日本語C++宣言ファイルの内容です。
#日本語定義 整数型 "int"
#日本語定義 付号なし整数型 "unsigned int"
#日本語定義 長い整数型 "long int"
#日本語定義 短い整数型 "short int"
#日本語定義 サイズ型 "size_t"
#日本語定義 文字型 "char"
#日本語定義 文字列型 "string"
#日本語定義 実数型 "float"
#日本語定義 論理型 "bool"
#日本語定義 整数ベクトル計算型 "__m128i"
#日本語定義 実数ベクトル計算型 "__m128"
#日本語定義 整数への番地型| "int *"
#日本語定義 文字への番地型| "char *"
#日本語定義 実数への番地型| "float *"
#日本語定義 定数指定 "const"
#日本語定義 外部定義 "extern"
#日本語定義 型なし "void"
#日本語定義 構造体 "struct"
#日本語定義 共用体 "union"
#日本語定義 仲間の集まり "class"
#日本語定義 全域で使用可 "public"
#日本語定義 仲間内で使用可 "private"
#日本語定義 派生の仲間まで使用可 "protected"
#日本語定義 直接出入可 "friend"
#日本語定義 である、 "::"
#日本語定義 スコープ解決 "::"
#日本語定義 標準的な名前空間 "using namespace std"
#日本語定義 内部埋め込み "inline"
#日本語定義 文字列の仲間 "string"
#日本語定義 もし "if"
#日本語定義 それ以外 "else"
#日本語定義 戻る "return"
#日本語定義 繰り返し "while"
#日本語定義 反復 "for"
#日本語定義 振り分け "switch"
#日本語定義 場合分け "case"
#日本語定義 中断する "break"
#日本語定義 場合分け終了 "break"
#日本語定義 どれでもない "default"
#日本語定義 読み込む "cin"
#日本語定義 表示する "cout"
#日本語定義 印字する "cout"
#日本語定義 表示(注意)する "cerr"
#日本語定義 改行 "endl"
#日本語定義 入力反復子 "inserter"
#日本語定義 文字の特性 "char_traits"
#日本語定義 集合ひな型 "set<int>"
#日本語定義 リストひな型 "list<int>"
#日本語定義 ベクターひな型 "vector"
#日本語定義 複写 "copy"
#日本語定義 割り当て子 "allocator"
#日本語定義 の最初 ".begin()"
#日本語定義 の最後 ".end()"
#日本語定義 ← "<<"
#日本語定義 → ">>"
#日本語定義 番地| "*"
#日本語定義 参照| "&"
#日本語定義 中味| "*"
#日本語定義 かつ "&&"
#日本語定義 または "||"
#日本語定義 ならば " "
#日本語定義 真 "true"
#日本語定義 偽 "false"
#日本語定義 はじまり "main"
#日本語定義 通常終了 "return 0"
#日本語定義 異常終了 "return 1"
#日本語定義 強制終了 "exit(1)"
#日本語定義 入出力の仲間を呼ぶ "#include <iostream>"
#日本語定義 ファイル操作の仲間を呼ぶ "#include <fstream>"
#日本語定義 文字列入出力の仲間を呼ぶ "#include <sstream>"
#日本語定義 数学の仲間を呼ぶ "#include <math.h>"
#日本語定義 文字列の仲間を呼ぶ "#include <string>"
#日本語定義 ベクトルの仲間を呼ぶ "#include <vector>"
#日本語定義 集合の仲間を呼ぶ "#include <set>"
#日本語定義 アルゴリズムの仲間を呼ぶ "#include <algorithm>"
#日本語定義 反復子の仲間を呼ぶ "#include <iterator>"
これ以降の例題では、プログラム内に上記の日本語定義の部分はありません。
πを検証する
はじめに、例題W2-1として西暦年を入力し、その年がうるう年かどうかを判定するプログラムをcpp_ex1.jcppとして示します。
今度のC++コンパイラのバージョン7.3の大きな特徴として、変数や関数名などに日本語がそのまま使えるようになったことが挙げられます。
そこで、プログラム中でも今まで日本語カスタマイザーの自動変数として定義していた日本語定義の部分は、そのまま直接プログラム中で使うことにします。
// 西暦を入力し、その年がうるう年かどうかを判定する
入出力の仲間を呼ぶ
//#define _BCC32C
#ifdef _BCC32C
#include
#endif
標準的な名前空間;
#日本語定義 うるう年である "true"
#日本語定義 うるう年ではない "false"
#日本語定義 がうるう年である "== true"
#日本語定義 剰余計算 "%%"
#日本語定義 が割り切れる "== 0"
#日本語定義 どちらか大きい方 "max"
論理型 うるう年の判定( 整数型 );
内部埋め込み 論理型 うるう年の判定( 整数型 その年 )
{
もし ( ( その年 剰余計算 400 ) が割り切れる ) ならば 戻る( うるう年である );
それ以外 もし ( ( その年 剰余計算 100 ) が割り切れる ) ならば 戻る( うるう年ではない );
それ以外 もし ( ( その年 剰余計算 4 ) が割り切れる ) ならば 戻る( うるう年である );
それ以外 ならば 戻る( うるう年ではない );
}
整数型 はじまり( 型なし )
{
整数型 年のデータ = 1;
印字する ← "年(西暦)を入力してください。(1以上の数字)" ← 改行;
読み込む → 年のデータ;
年のデータ = どちらか大きい方( 年のデータ, 1 ); // 必ず入力値を1以上とする。
印字する ← "西暦" ← 年のデータ ← "年は";
印字する ← ( うるう年の判定(年のデータ) ? "うるう年である。":"うるう年でない。" ) ← 改行 ;
return 0;
}
例題W2-1
西暦2000年問題という、うるう年の判定について、以前随分と話題になったことを覚えていらっしゃる方も多いと思いますが、うるう年かどうかの判断もややこしく、判断の順番を間違えないようにする必要があるようです。
また、C++言語になって、今までの/*...*/に加えて、コメントに//が使用できますので、FLEXの日本語解析プログラムもC++言語のコメント対応に変更しました。さらに変数の宣言は、変数を使う場所で宣言することができるのもC++言語の特徴ではないでしょうか。これは次のようなC++言語のコードに展開されます。
// 西暦を入力し、その年がうるう年かどうかを判定する
#include <iostream>
//#define _BCC32C
#ifdef _BCC32C
#include <algorithm>
#endif
using namespace std;
bool うるう年の判定( int );
inline bool うるう年の判定( int その年 )
{
if ( ( その年 % 400 ) == 0 ) return( true );
else if ( ( その年 % 100 ) == 0 ) return( false );
else if ( ( その年 % 4 ) == 0 ) return( true );
else return( false );
}
int main( void )
{
int 年のデータ = 1;
cout << "年(西暦)を入力してください。(1以上の数字)" << endl;
cin >> 年のデータ;
年のデータ = max( 年のデータ, 1 ); // 必ず入力値を1以上とする。
cout << "西暦" << 年のデータ << "年は";
cout << ( うるう年の判定(年のデータ) ? "うるう年である。":"うるう年でない。" ) << endl ;
return 0;
}
例題W2-1を展開したもの
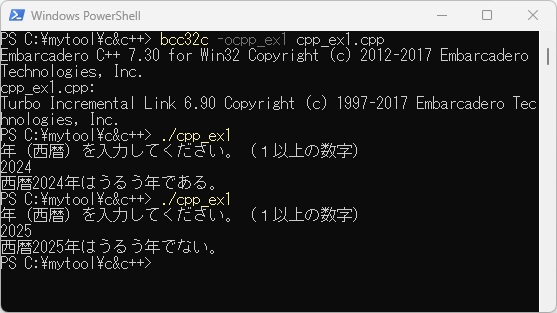
このcpp_ex1.jcppをWSL上でコ日本語カスタマイザーで処理し、コンパイル、リンクします。下記は例2-1のプログラムを実行させ、西暦を2024年、2025年としたときの結果ですが、最小値は1(西暦1年)にしています。
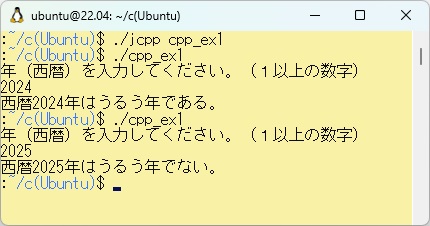
PowerShell上のbcc32c v7.3ではmax関数を利用するために#include <algorithm>を宣言します。このため、WSL上のcpp_ex1.jcppをエディタを使って//#define _BCC32Cのコメント//を外して、「./jcpp cpp_ex1 -c」でコンパイルだけして、bcc32c用のcpp_ex1.cppを作成します。
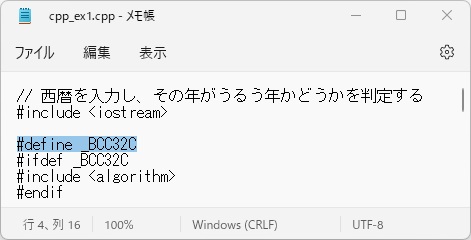
次に、PowerShell上にcpp_ex1.cppをコピーします。ここで「$Env:Ubuntu」はWSL上で、cpp_ex1.cppファイルの場所をあらかじめ設定しています。
また、PowerShell上のbcc32cでcpp_ex1.cppをコンパイル、リンクし、プログラムを実行します。
次の例は、C++言語の目玉ともいうべき「クラス」を使ってみたものです。ここでは「クラス」を「仲間の集まり」という日本語で置き換えてみました。C言語の構造体が変数の集まりとして定義されていたのに対して、C++言語のクラスは変数だけではなく、関数も定義できるようにしてあるのが特徴といえるのではないでしょうか。 ここでもプログラム中のクラス名にそのまま日本語を使ってみます。
この例題W2─2では、簡単な計算を行う関数を「基本計算の仲間」として定義してあります。この関数はクラスのメンバー関数と呼ばれていますが、これを内部埋め込み(インライン)関数としました。
// 簡単な計算をする仲間の集まり(クラス)を作り、計算してみる
入出力の仲間を呼ぶ
標準的な名前空間;
仲間の集まり 基本計算の仲間
{
全域で使用可:
基本計算の仲間(型なし) { /* 表示する ← "基本計算の対象(オブジェクト)を組み立てる" ← 改行; */ };
実数型 足す ( 実数型, 実数型 );
実数型 引く ( 実数型, 実数型 );
実数型 掛ける( 実数型, 実数型 );
実数型 割る ( 実数型, 実数型 );
整数型 余り ( 整数型, 整数型 );
論理型 論理積( 論理型, 論理型 );
論理型 論理和( 論理型, 論理型 );
~基本計算の仲間(型なし) { /* 表示する ← "基本計算の対象(オブジェクト)を消滅させる" ← 改行; */ };
};
内部埋め込み 実数型 基本計算の仲間である、足す ( 実数型 引数1, 実数型 引数2 ) { 戻る( 引数1 + 引数2 ); };
内部埋め込み 実数型 基本計算の仲間である、引く ( 実数型 引数1, 実数型 引数2 ) { 戻る( 引数1 - 引数2 ); };
内部埋め込み 実数型 基本計算の仲間である、掛ける( 実数型 引数1, 実数型 引数2 ) { 戻る( 引数1 * 引数2 ); };
内部埋め込み 実数型 基本計算の仲間である、割る ( 実数型 引数1, 実数型 引数2 ) { 戻る( 引数1 / 引数2 ); };
内部埋め込み 整数型 基本計算の仲間である、余り ( 整数型 引数1, 整数型 引数2 ) { 戻る( 引数1 % 引数2 ); };
内部埋め込み 論理型 基本計算の仲間である、論理積( 論理型 引数1, 論理型 引数2 ) { 戻る( 引数1 && 引数2 ); };
内部埋め込み 論理型 基本計算の仲間である、論理和( 論理型 引数1, 論理型 引数2 ) { 戻る( 引数1 || 引数2 ); };
#日本語定義 入力文字数
#日本語定義 入力文字列
#日本語定義 文字列から実数へ "atof"
整数型 はじまり(整数型 入力数,文字への番地型|入力文字列[])
{
実数型 引数1,引数2;
もし ( 入力数 != 4 ) 異常終了;
引数1 = 文字列から実数へ( 入力文字列[1] );
引数2 = 文字列から実数へ( 入力文字列[3] );
基本計算の仲間 計算くん;
表示する ← " "← 引数1 ← " "← 入力文字列[2] ←" "← 引数2 ← " = " ;
振り分け( 入力文字列[2][0] ) {
場合分け '+': 表示する ← 計算くん.足す ( 引数1, 引数2 ) ; break;
場合分け '-': 表示する ← 計算くん.引く ( 引数1, 引数2 ) ; break;
場合分け '*': 表示する ← 計算くん.掛ける ( 引数1, 引数2 ) ; break;
場合分け '/': 表示する ← 計算くん.割る ( 引数1, 引数2 ) ; break;
場合分け '%': 表示する ← 計算くん.余り ( 引数1, 引数2 ) ; break;
場合分け 'A': 表示する ← ( 計算くん.論理積( 引数1, 引数2 ) ? "1" : "0" ) ; break;
場合分け 'U': 表示する ← ( 計算くん.論理和( 引数1, 引数2 ) ? "1" : "0" ) ; break;
どれでもない: 表示する ← "演算子が未定義です" ; break;
}
表示する ← 改行;
通常終了;
}
例題W2-2
さらに、C++言語では入出力ストリーム(iostreamクラスライブラリ)で使われる">>"と"<<"記号が入出力ストリーム演算子として使われていますが、これらはビットシフト演算子と兼用してあるかのように見えます。しかし、同じ記号を別の意味で使用すると混乱を招きやすいということもあり、これを「→」と「←」の2バイト記号で日本語定義として置き換えてみました。例2─2は次のようなC++言語のコードに展開されます。
// 簡単な計算をする仲間の集まり(クラス)を作り、計算してみる
#include <iostream>
using namespace std;
class 基本計算の仲間
{
public:
基本計算の仲間(void) { /* 表示する ← "基本計算の対象(オブジェクト)を組み立てる" ← 改行; */ };
float 足す ( float, float );
float 引く ( float, float );
float 掛ける( float, float );
float 割る ( float, float );
int 余り ( int, int );
bool 論理積( bool, bool );
bool 論理和( bool, bool );
~基本計算の仲間(void) { /* 表示する ← "基本計算の対象(オブジェクト)を消滅させる" ← 改行; */ };
};
inline float 基本計算の仲間::足す ( float 引数1, float 引数2 ) { return( 引数1 + 引数2 ); };
inline float 基本計算の仲間::引く ( float 引数1, float 引数2 ) { return( 引数1 - 引数2 ); };
inline float 基本計算の仲間::掛ける( float 引数1, float 引数2 ) { return( 引数1 * 引数2 ); };
inline float 基本計算の仲間::割る ( float 引数1, float 引数2 ) { return( 引数1 / 引数2 ); };
inline int 基本計算の仲間::余り ( int 引数1, int 引数2 ) { return( 引数1 % 引数2 ); };
inline bool 基本計算の仲間::論理積( bool 引数1, bool 引数2 ) { return( 引数1 && 引数2 ); };
inline bool 基本計算の仲間::論理和( bool 引数1, bool 引数2 ) { return( 引数1 || 引数2 ); };
int main(int 入力数,char *jp_str_1[])
{
float 引数1,引数2;
if ( 入力数 != 4 ) return 1;
引数1 = atof( jp_str_1[1] );
引数2 = atof( jp_str_1[3] );
基本計算の仲間 計算くん;
cout << " "<< 引数1 << " "<< jp_str_1[2] <<" "<< 引数2 << " = " ;
switch( jp_str_1[2][0] ) {
case '+': cout << 計算くん.足す ( 引数1, 引数2 ) ; break;
case '-': cout << 計算くん.引く ( 引数1, 引数2 ) ; break;
case '*': cout << 計算くん.掛ける ( 引数1, 引数2 ) ; break;
case '/': cout << 計算くん.割る ( 引数1, 引数2 ) ; break;
case '%': cout << 計算くん.余り ( 引数1, 引数2 ) ; break;
case 'A': cout << ( 計算くん.論理積( 引数1, 引数2 ) ? "1" : "0" ) ; break;
case 'U': cout << ( 計算くん.論理和( 引数1, 引数2 ) ? "1" : "0" ) ; break;
default: cout << "演算子が未定義です" ; break;
}
cout << endl;
return 0;
}
例題W2-2を展開したもの
例2─2を実行した結果を以下に示します。「計算くん」という「基本計算の仲間」クラスの対象(オブジェクト)が生成されると、最初にコンストラクタと呼ばれる部分が起動します。あとは対象(オブジェクト)のメンバー関数を呼ぶだけで、簡単な計算を行うことができます。最後にデストラクタと呼ばれる部分が起動し、対象(オブジェクト)が消滅します。
このcpp_ex2.jcppをWSL上でコ日本語カスタマイザーで処理し、コンパイル、リンクします。下記は例2-2のプログラムを実行させ、和差積商(+ - * /)、論理和(U)、論理積(A)の演算を行いました。また、入力は「数値 演算子 数値」という形式で行うようにしました。
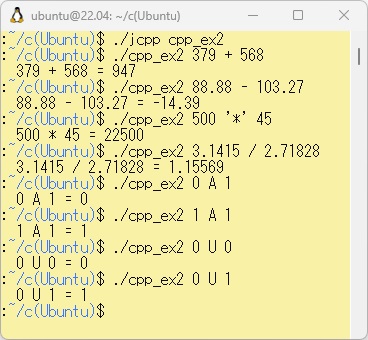
次に、PowerShell上にcpp_ex2.cppをコピーします。ここで「$Env:Ubuntu」はWSL上でのcpp_ex2.cppファイルの場所をあらかじめ設定しています。これをコンパイル、リンクして実行した例を以下に示します。
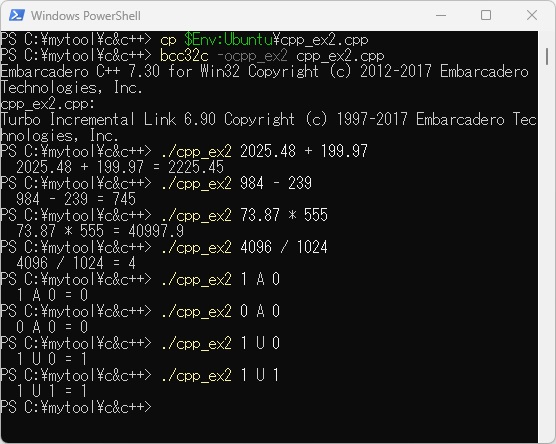
C言語編でも少し述べましたが、C++言語では「参照型」という新しい型が定義されています。これには「&」というアドレスを表す記号が使われています。 次の例題W2─3では、その参照型「参照|」で宣言した変数がどのような振る舞いをするのかを見てみます。 また、ポインタを表す「*」記号について、やはりC言語編と同じように「番地|」、「中味|」という日本語定義で表記したときに、どのように記述されるのかも併せて見ていきます。
// 参照型とポインタ、配列についての例
入出力の仲間を呼ぶ
標準的な名前空間;
整数型 はじまり(型なし)
{
整数型 実際の数;
整数型 参照|その分身 = 実際の数; // 宣言文で参照型を定義します
実際の数 = 2024; // 実際の数に定数を代入すると、その分身にも代入されます。
表示する ← "参照型の例 参照型で「実際の数」と「その分身」を定義する" ← 改行;
表示する ← "実際の数="← 実際の数 ← " その分身=" ← その分身 ← 改行← 改行;
--その分身; // その分身を減少させると、実際の数も減ります。
表示する ← "「その分身」を1減らすと「実際の数」も1減る" ← 改行;
表示する ← "実際の数="← 実際の数 ← " その分身=" ← その分身 ← 改行← 改行;
実際の数+=2; // 実際の数を増加させると、その分身も増えます。
表示する ← "「実際の数」を2増やすと「その分身も2増える」" ← 改行;
表示する ← "実際の数="← 実際の数 ← " その分身=" ← その分身 ← 改行← 改行;
整数への番地型|もう一つの数; // もう一つの数は整数型への番地であると定義します。
表示する ← "ポインタの例" ← 改行;
表示する ← "整数への番地型「もう一つの数」が「その分身」を参照できるようにする" ← 改行;
もう一つの数 = 参照|その分身; // もう一つの数がその分身を参照できるようにします。
表示する ←"もう一つの数="← 中味|もう一つの数 ← 改行 ← 改行;
表示する ← "配列の例 整数型配列「他の数」を定義する" ← 改行;
整数型 他の数[2] = {180,8888}; // 他の数は整数型の初期値を持った配列を表します。
表示する ← "他の数=" ← 他の数[0] ← " "←他の数[1]← 改行← 改行;
表示する ← "整数への番地型「もう一つの数」が配列「他の数」を参照できるようにする" ← 改行;
もう一つの数 = 参照|他の数[0]; // 配列の要素に対応する番地をもう一つの数に代入します。
表示する ← "もう一つの数=" ← 中味|もう一つの数 ← " ";
もう一つの数 = 参照|他の数[1];
表示する ← 中味|もう一つの数 ← 改行;
通常終了;
}
例題W2-3
このように実際の数(通常の変数)と、その分身(参照型変数)のどちらを変えても同じように操作されることが分かります。これは次のようなC++言語のコードに展開されます。
// 参照型とポインタ、配列についての例
#include <iostream>
using namespace std;
int main(void)
{
int 実際の数;
int &その分身 = 実際の数; // 宣言文で参照型を定義します
実際の数 = 2024; // 実際の数に定数を代入すると、その分身にも代入されます。
cout << "参照型の例 参照型で「実際の数」と「その分身」を定義する" << endl;
cout << "実際の数="<< 実際の数 << " その分身=" << その分身 << endl<< endl;
--その分身; // その分身を減少させると、実際の数も減ります。
cout << "「その分身」を1減らすと「実際の数」も1減る" << endl;
cout << "実際の数="<< 実際の数 << " その分身=" << その分身 << endl<< endl;
実際の数+=2; // 実際の数を増加させると、その分身も増えます。
cout << "「実際の数」を2増やすと「その分身も2増える」" << endl;
cout << "実際の数="<< 実際の数 << " その分身=" << その分身 << endl<< endl;
int *もう一つの数; // もう一つの数は整数型への番地であると定義します。
cout << "ポインタの例" << endl;
cout << "整数への番地型「もう一つの数」が「その分身」を参照できるようにする" << endl;
もう一つの数 = &その分身; // もう一つの数がその分身を参照できるようにします。
cout <<"もう一つの数="<< *もう一つの数 << endl << endl;
cout << "配列の例 整数型配列「他の数」を定義する" << endl;
int 他の数[2] = {180,8888}; // 他の数は整数型の初期値を持った配列を表します。
cout << "他の数=" << 他の数[0] << " "<<他の数[1]<< endl<< endl;
cout << "整数への番地型「もう一つの数」が配列「他の数」を参照できるようにする" << endl;
もう一つの数 = &他の数[0]; // 配列の要素に対応する番地をもう一つの数に代入します。
cout << "もう一つの数=" << *もう一つの数 << " ";
もう一つの数 = &他の数[1];
cout << *もう一つの数 << endl;
return 0;
}
例題W2-3を展開したもの
例題W2-3のプログラムをWSL上で実行させた結果は以下に示します。
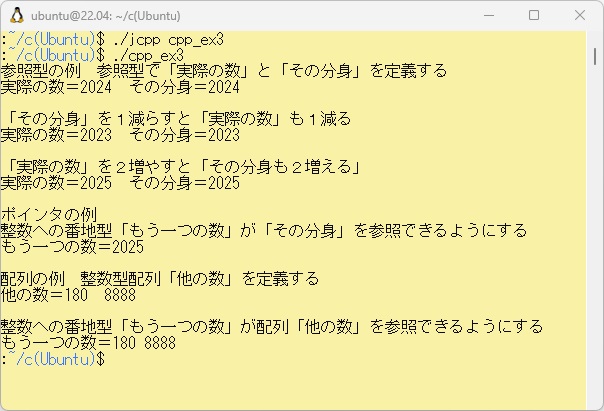
次に、PowerShell上にcpp_ex3.cppをコピーします。ここで「$Env:Ubuntu」はWSL上でのcpp_ex3.cppファイルの場所をあらかじめ設定しています。これをコンパイル、リンクして実行した例を以下に示します。
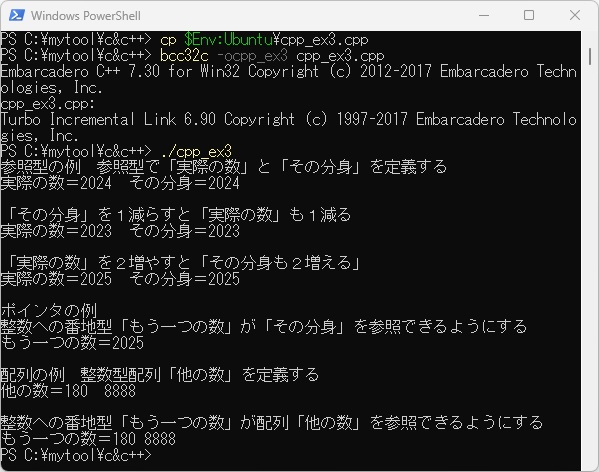
今回はC言語編と同じように「&」、「*」を日本語定義で「参照|」、「整数への番地型|」、「中味|」と置き換えて使ってみましたが、C++言語でも特に問題なく使えるのではないでしょうか。
話は変わりますが、以前はC++言語でのmain関数が特に値を返さない場合には、voidと書いておけば処理系から文句が出ることはありませんでしたが、現在のC++言語では明確にエラーとみなされます。従ってmain関数をint型として宣言しておき、最後に「return 終了コード」としています。
次は例題W2─2で簡単な四則演算と論理演算程度の計算を行う仲間の集まり(クラス)を定義しましたが、これを少し発展させてみたいと思います。その機能拡張として、平方根、累乗、消費税計算の機能を加えてみます。
新しい計算の仲間は、応用計算を基本計算から継承させる仲間の集まり(クラス)として定義しています。また今回はクラス名を日本語カスタマイザーの自動変数定義で行いました。
// 応用計算を基本計算から継承させる仲間の集まり(クラス)を作る
入出力の仲間を呼ぶ
数学の仲間を呼ぶ
標準的な名前空間;
仲間の集まり 基本計算の仲間
{
全域で使用可:
基本計算の仲間(型なし) { /* 表示する ← "基本計算の対象を組み立てる" ← 改行; */ };
実数型 足す ( 実数型, 実数型 );
実数型 引く ( 実数型, 実数型 );
実数型 掛ける( 実数型, 実数型 );
実数型 割る ( 実数型, 実数型 );
整数型 余り ( 整数型, 整数型 );
論理型 論理積( 論理型, 論理型 );
論理型 論理和( 論理型, 論理型 );
~基本計算の仲間(型なし) { /* 表示する ← "基本計算の対象を消滅させる" ← 改行; */ };
};
仲間の集まり 応用計算の仲間 : 全域で使用可 基本計算の仲間
{
全域で使用可:
応用計算の仲間(型なし) { /* 表示する ← "応用計算の仲間の対象を組み立てる" ← 改行; */ };
実数型 SINを求める( 実数型 引数一 ) ;
実数型 COSを求める( 実数型 引数一 ) ;
実数型 TANを求める( 実数型 引数一 ) ;
実数型 数値根を求める( 実数型 引数一 ) ;
実数型 累乗を求める( 実数型 引数一, 実数型 引数二 ) ;
整数型 税込み価格を求める( 整数型 引数一 ) ;
~応用計算の仲間(型なし) { /* 表示する ← "応用計算の仲間の対象を消滅させる" ← 改行; */ };
};
内部埋め込み 実数型 基本計算の仲間である、足す ( 実数型 引数1, 実数型 引数2 ) { 戻る( 引数1 + 引数2 ); };
内部埋め込み 実数型 基本計算の仲間である、引く ( 実数型 引数1, 実数型 引数2 ) { 戻る( 引数1 - 引数2 ); };
内部埋め込み 実数型 基本計算の仲間である、掛ける( 実数型 引数1, 実数型 引数2 ) { 戻る( 引数1 * 引数2 ); };
内部埋め込み 実数型 基本計算の仲間である、割る ( 実数型 引数1, 実数型 引数2 ) { 戻る( 引数1 / 引数2 ); };
内部埋め込み 整数型 基本計算の仲間である、余り ( 整数型 引数1, 整数型 引数2 ) { 戻る( 引数1 % 引数2 ); };
内部埋め込み 論理型 基本計算の仲間である、論理積( 論理型 引数1, 論理型 引数2 ) { 戻る( 引数1 && 引数2 ); };
内部埋め込み 論理型 基本計算の仲間である、論理和( 論理型 引数1, 論理型 引数2 ) { 戻る( 引数1 || 引数2 ); };
#日本語定義 入力文字列
#日本語定義 文字列から実数へ "atof"
#日本語定義 正弦値 "sin"
#日本語定義 余弦値 "cos"
#日本語定義 正接値 "tan"
#日本語定義 平方根 "sqrt"
#日本語定義 累乗 "pow"
#日本語定義 切り捨て "floor"
#日本語定義 物品消費税率 "1.1"
実数型 応用計算の仲間::SINを求める( 実数型 引数一)
{
戻る( 正弦値(引数一) );
};
実数型 応用計算の仲間::COSを求める( 実数型 引数一)
{
戻る( 余弦値(引数一) );
};
実数型 応用計算の仲間::TANを求める( 実数型 引数一)
{
戻る( 正接値(引数一) );
};
実数型 応用計算の仲間::数値根を求める( 実数型 引数一)
{
戻る( 平方根(引数一) );
};
実数型 応用計算の仲間::累乗を求める( 実数型 引数一, 実数型 引数二 )
{
戻る( 累乗(引数一,引数二) );
};
整数型 応用計算の仲間::税込み価格を求める( 整数型 引数一)
{
戻る( 切り捨て(引数一 * 物品消費税率) );
};
整数型 はじまり(整数型 入力数,文字への番地型|入力文字列[])
{
実数型 引数1,引数2;
もし ( 入力数 == 3 ) {
引数1 = 文字列から実数へ( 入力文字列[1] );
表示する ← " "← 引数1 ← " "← 入力文字列[2] ← " = " ;
}
それ以外 もし ( 入力数 == 4 ) {
引数1 = 文字列から実数へ( 入力文字列[1] );
引数2 = 文字列から実数へ( 入力文字列[3] );
表示する ← " "← 引数1 ← " "← 入力文字列[2] ←" "← 引数2 ← " = " ;
}
それ以外 { 異常終了;}
応用計算の仲間 計算くん;
振り分け( 入力文字列[2][0] ) {
場合分け '+': 表示する ← 計算くん.足す ( 引数1, 引数2 ) ; break;
場合分け '-': 表示する ← 計算くん.引く ( 引数1, 引数2 ) ; break;
場合分け '*': 表示する ← 計算くん.掛ける ( 引数1, 引数2 ) ; break;
場合分け '/': 表示する ← 計算くん.割る ( 引数1, 引数2 ) ; break;
場合分け '%': 表示する ← 計算くん.余り ( 引数1, 引数2 ) ; break;
場合分け 'A': 表示する ← ( 計算くん.論理積( 引数1, 引数2 ) ? "1" : "0" ) ; break;
場合分け 'U': 表示する ← ( 計算くん.論理和( 引数1, 引数2 ) ? "1" : "0" ) ; break;
場合分け 'S': 表示する ← 計算くん.SINを求める( 引数1 / 360 * 6.283185 ) ; break;
場合分け 'C': 表示する ← 計算くん.COSを求める( 引数1 / 360 * 6.283185 ) ; break;
場合分け 'T': 表示する ← 計算くん.TANを求める( 引数1 / 360 * 6.283185 ) ; break;
場合分け 'R': 表示する ← 計算くん.数値根を求める( 引数1 ) ; break;
場合分け '^': 表示する ← 計算くん.累乗を求める( 引数1, 引数2 ) ; break;
場合分け 'Z': 表示する ← 計算くん.税込み価格を求める( 引数1 ) ; break;
どれでもない: 表示する ← "演算子が未定義です" ; break;
}
表示する ← 改行;
通常終了;
}
例題W2─4
例2─4の日本語定義プログラムは次のようなC++言語のコードに展開されます。
// 応用計算を基本計算から継承させる仲間の集まり(クラス)を作る
#include <iostream>
#include <math.h>
using namespace std;
class 基本計算の仲間
{
public:
基本計算の仲間(void) { /* 表示する ← "基本計算の対象を組み立てる" ← 改行; */ };
float 足す ( float, float );
float 引く ( float, float );
float 掛ける( float, float );
float 割る ( float, float );
int 余り ( int, int );
bool 論理積( bool, bool );
bool 論理和( bool, bool );
~基本計算の仲間(void) { /* 表示する ← "基本計算の対象を消滅させる" ← 改行; */ };
};
class 応用計算の仲間 : public 基本計算の仲間
{
public:
応用計算の仲間(void) { /* 表示する ← "応用計算の仲間の対象を組み立てる" ← 改行; */ };
float SINを求める( float 引数一 ) ;
float COSを求める( float 引数一 ) ;
float TANを求める( float 引数一 ) ;
float 数値根を求める( float 引数一 ) ;
float powを求める( float 引数一, float 引数二 ) ;
int 税込み価格を求める( int 引数一 ) ;
~応用計算の仲間(void) { /* 表示する ← "応用計算の仲間の対象を消滅させる" ← 改行; */ };
};
inline float 基本計算の仲間::足す ( float 引数1, float 引数2 ) { return( 引数1 + 引数2 ); };
inline float 基本計算の仲間::引く ( float 引数1, float 引数2 ) { return( 引数1 - 引数2 ); };
inline float 基本計算の仲間::掛ける( float 引数1, float 引数2 ) { return( 引数1 * 引数2 ); };
inline float 基本計算の仲間::割る ( float 引数1, float 引数2 ) { return( 引数1 / 引数2 ); };
inline int 基本計算の仲間::余り ( int 引数1, int 引数2 ) { return( 引数1 % 引数2 ); };
inline bool 基本計算の仲間::論理積( bool 引数1, bool 引数2 ) { return( 引数1 && 引数2 ); };
inline bool 基本計算の仲間::論理和( bool 引数1, bool 引数2 ) { return( 引数1 || 引数2 ); };
float 応用計算の仲間::SINを求める( float 引数一)
{
return( sin(引数一) );
};
float 応用計算の仲間::COSを求める( float 引数一)
{
return( cos(引数一) );
};
float 応用計算の仲間::TANを求める( float 引数一)
{
return( tan(引数一) );
};
float 応用計算の仲間::数値根を求める( float 引数一)
{
return( sqrt(引数一) );
};
float 応用計算の仲間::powを求める( float 引数一, float 引数二 )
{
return( pow(引数一,引数二) );
};
int 応用計算の仲間::税込み価格を求める( int 引数一)
{
return( floor(引数一 * 1.1) );
};
int main(int 入力数,char *jp_str_0[])
{
float 引数1,引数2;
if ( 入力数 == 3 ) {
引数1 = atof( jp_str_0[1] );
cout << " "<< 引数1 << " "<< jp_str_0[2] << " = " ;
}
else if ( 入力数 == 4 ) {
引数1 = atof( jp_str_0[1] );
引数2 = atof( jp_str_0[3] );
cout << " "<< 引数1 << " "<< jp_str_0[2] <<" "<< 引数2 << " = " ;
}
else { return 1;}
応用計算の仲間 計算くん;
switch( jp_str_0[2][0] ) {
case '+': cout << 計算くん.足す ( 引数1, 引数2 ) ; break;
case '-': cout << 計算くん.引く ( 引数1, 引数2 ) ; break;
case '*': cout << 計算くん.掛ける ( 引数1, 引数2 ) ; break;
case '/': cout << 計算くん.割る ( 引数1, 引数2 ) ; break;
case '%': cout << 計算くん.余り ( 引数1, 引数2 ) ; break;
case 'A': cout << ( 計算くん.論理積( 引数1, 引数2 ) ? "1" : "0" ) ; break;
case 'U': cout << ( 計算くん.論理和( 引数1, 引数2 ) ? "1" : "0" ) ; break;
case 'S': cout << 計算くん.SINを求める( 引数1 / 360 * 6.283185 ) ; break;
case 'C': cout << 計算くん.COSを求める( 引数1 / 360 * 6.283185 ) ; break;
case 'T': cout << 計算くん.TANを求める( 引数1 / 360 * 6.283185 ) ; break;
case 'R': cout << 計算くん.数値根を求める( 引数1 ) ; break;
case '^': cout << 計算くん.powを求める( 引数1, 引数2 ) ; break;
case 'Z': cout << 計算くん.税込み価格を求める( 引数1 ) ; break;
default: cout << "演算子が未定義です" ; break;
}
cout << endl;
return 0;
}
例題W2-4を展開したもの
例題W2-4のプログラムを実行させ、正弦関数(S)、余弦関数(C)、正接関数(T)、平方根(R)、累乗(^)、消費税込み(Z)の計算結果例を示します。例題W2-4で既に行った基本計算結果は割愛してあます。この他、C++言語では、さまざまな組み込み関数が用意されていますが、その一部を使用しています。入力は「数値 演算子 数値」または、「数値 演算子」という形式で行うようにしました。

次に、PowerShell上にcpp_ex4.cppをコピーします。ここで「$Env:Ubuntu」はWSL上でのcpp_ex4.cppファイルの場所をあらかじめ設定しています。これをコンパイル、リンクして実行した例を以下に示します。
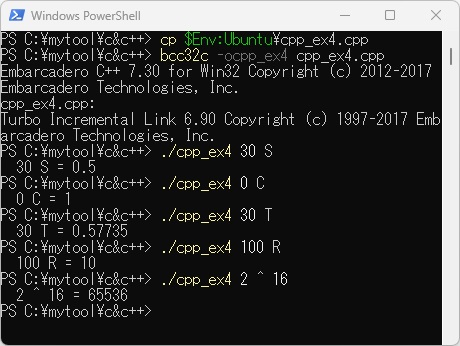
このようにオブジェクト指向言語といわれるC++言語では、仲間の集まり(クラス)を継承することで、今あるソフトウェア財産をそのまま利用して無駄なく機能拡張ができます。さらに対象(オブジェクト)の生成では、まず基本(親)となる仲間の集まり(クラス)が生成され、次に継承(子)された仲間の集まり(クラス)が生成されることが、この実行結果により分かります。また、対象(オブジェクト)の消滅では、逆に継承(子)された仲間の集まり(クラス)が消滅して、最後に基本(親)となる仲間の集まり(クラス)が消滅しますので、生成と消滅はちょうど入れ子のような格好になっています。
ここでは、intelx86系プロセッサのSSE(Streaming Single-instruction,multiple-data Extentions)機能を使ってC++言語で簡易的な並列計算をやってみます。まず、よく普及しているx86系PC上でSSE命令を実行できるプロセッサかどうかを確認します。このため、WSL上で「lscpu | grep 'sse'」でSSE関連のフラグを見て、SSE、SSE2、SSE3、SSE4、SSE4.2が利用できることを確認しました。

2つの配列にそれぞれ4つの数値を入力し、これをSSE命令で並列に加減乗除する日本語プログラム例題W2-5を以下に示します。
入出力の仲間を呼ぶ
//#define _BCC32C
#ifdef _BCC32C
#define __SSE2__
#define __SSE__
#define __MMX__
#include <emmintrin.h> // SSE命令セットのヘッダー(BCC32C)
#else
#include <immintrin.h> // SSE命令セットのヘッダー(GCC)
#endif
標準的な名前空間;
#日本語定義 ベクトルの加算 "_mm_add_ps"
#日本語定義 ベクトルの減算 "_mm_sub_ps"
#日本語定義 ベクトルの乗算 "_mm_mul_ps"
#日本語定義 ベクトルの除算 "_mm_div_ps"
#日本語定義 引数をセット "_mm_load_ps"
#日本語定義 計算結果を代入 "_mm_store_ps"
#日本語定義 アライメント指定 "alignas" // バイトアライメントを指定
型なし 並列加算する(実数への番地型|引数1, 実数への番地型|引数2, 実数への番地型| 計算結果) {
実数ベクトル計算型 ベクトル1 = 引数をセット(引数1), ベクトル2 = 引数をセット(引数2);
計算結果を代入(計算結果, ベクトルの加算(ベクトル1, ベクトル2));
}
型なし 並列減算する(実数への番地型|引数1, 実数への番地型|引数2, 実数への番地型| 計算結果) {
実数ベクトル計算型 ベクトル1 = 引数をセット(引数1), ベクトル2 = 引数をセット(引数2) ;
計算結果を代入(計算結果, ベクトルの減算(ベクトル1, ベクトル2));
}
型なし 並列乗算する(実数への番地型|引数1, 実数への番地型|引数2, 実数への番地型| 計算結果) {
実数ベクトル計算型 ベクトル1 = 引数をセット( 引数1), ベクトル2 = 引数をセット(引数2);
計算結果を代入(計算結果, ベクトルの乗算(ベクトル1, ベクトル2));
}
型なし 並列除算する(実数への番地型|引数1, 実数への番地型|引数2, 実数への番地型| 計算結果) {
実数ベクトル計算型 ベクトル1 = 引数をセット(引数1), ベクトル2 = 引数をセット(引数2);
計算結果を代入(計算結果,ベクトルの除算(ベクトル1, ベクトル2));
}
整数型 はじまり() {
アライメント指定(16) 実数型 引数1[4],引数2[4],計算結果[4];
表示する ← "最初の4つの数を入力してください: " ← 改行;
読み込む → 引数1[0] → 引数1[1] → 引数1[2] → 引数1[3];
表示する ← "次の4つの数を入力してください: " ← 改行;
読み込む → 引数2[0] → 引数2[1] → 引数2[2] → 引数2[3];
並列加算する(引数1, 引数2, 計算結果);
表示する ← "並列加算結果: ";
反復 (短い整数型 回 = 0; 回 < 4; 回++) {
表示する ← 計算結果[回] ← " ";
}
表示する ← 改行;
並列減算する(引数1, 引数2, 計算結果);
表示する ← "並列減算結果: ";
反復 (短い整数型 回 = 0; 回 < 4; 回++) {
表示する ← 計算結果[回] ← " ";
}
表示する ← 改行;
並列乗算する(引数1, 引数2, 計算結果);
表示する ← "並列乗算結果: ";
反復 (短い整数型 回 = 0; 回 < 4; 回++) {
表示する ← 計算結果[回] ← " ";
}
表示する ← 改行;
並列除算する(引数1, 引数2, 計算結果);
表示する ← "並列除算結果: ";
反復 (短い整数型 回 = 0; 回 < 4; 回++) {
表示する ← 計算結果[回] ← " ";
}
表示する ← 改行;
通常終了;
}
例題W2─5
#include <iostream>
//#define _BCC32C
#ifdef _BCC32C
#define __SSE2__
#define __SSE__
#define __MMX__
#include <emmintrin.h> // SSE命令セットのヘッダー(BCC32C)
#else
#include <<immintrin.h> // SSE命令セットのヘッダー(GCC)
#endif
using namespace std;
// バイトアライメントを指定
void 並列加算する(float *引数1, float *引数2, float * 計算結果) {
__m128 ベクトル1 = _mm_load_ps(引数1), ベクトル2 = _mm_load_ps(引数2);
_mm_store_ps(計算結果, _mm_add_ps(ベクトル1, ベクトル2));
}
void 並列減算する(float *引数1, float *引数2, float * 計算結果) {
__m128 ベクトル1 = _mm_load_ps(引数1), ベクトル2 = _mm_load_ps(引数2) ;
_mm_store_ps(計算結果, _mm_sub_ps(ベクトル1, ベクトル2));
}
void 並列乗算する(float *引数1, float *引数2, float * 計算結果) {
__m128 ベクトル1 = _mm_load_ps( 引数1), ベクトル2 = _mm_load_ps(引数2);
_mm_store_ps(計算結果, _mm_mul_ps(ベクトル1, ベクトル2));
}
void 並列除算する(float *引数1, float *引数2, float * 計算結果) {
__m128 ベクトル1 = _mm_load_ps(引数1), ベクトル2 = _mm_load_ps(引数2);
_mm_store_ps(計算結果,_mm_div_ps(ベクトル1, ベクトル2));
}
int main() {
alignas(16) float 引数1[4],引数2[4],計算結果[4];
cout << "最初の4つの数を入力してください: " << endl;
cin >> 引数1[0] >> 引数1[1] >> 引数1[2] >> 引数1[3];
cout << "次の4つの数を入力してください: " << endl;
cin >> 引数2[0] >> 引数2[1] >> 引数2[2] >> 引数2[3];
並列加算する(引数1, 引数2, 計算結果);
cout << "並列加算結果: ";
for (short int 回 = 0; 回 < 4; 回++) {
cout << 計算結果[回] << " ";
}
cout << endl;
並列減算する(引数1, 引数2, 計算結果);
cout << "並列減算結果: ";
for (short int 回 = 0; 回 < 4; 回++) {
cout << 計算結果[回] << " ";
}
cout << endl;
並列乗算する(引数1, 引数2, 計算結果);
cout << "並列乗算結果: ";
for (short int 回 = 0; 回 < 4; 回++) {
cout << 計算結果[回] << " ";
}
cout << endl;
並列除算する(引数1, 引数2, 計算結果);
cout << "並列除算結果: ";
for (short int 回 = 0; 回 < 4; 回++) {
cout << 計算結果[回] << " ";
}
cout << endl;
return 0;
}
例題W2-5を展開したもの
WSL上でこの例題W2-5をコンパイルし、任意の値を入力した実行結果を以下に示します。
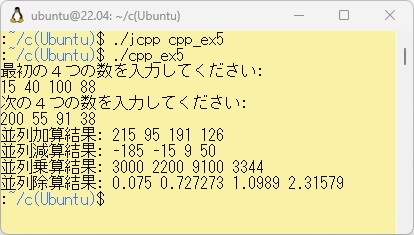
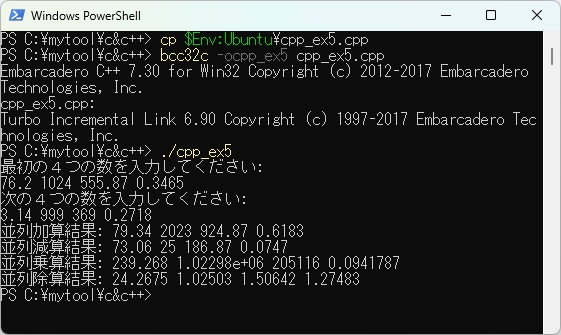
PowerShell上のbcc32cでこのプログラムを実行するために、WSL上のcpp_ex5.jcppをエディタを使って//#define _BCC32Cのコメント//を外して、「./jcpp cpp_ex5 -c」でコンパイルだけして、bcc32c用のcpp_ex5.cppを作成します。
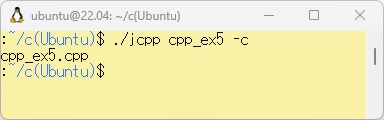
次に、PowerShell上にcpp_ex5.cppをコピーします。ここで「$Env:Ubuntu」はWSL上で、cpp_ex5.cppファイルの場所をあらかじめ設定しています。これをコンパイル、リンクして任意の値を入力した実行結果を以下に示します。
πを検証する2025年の円周率の最長桁は、2025年4月2日にカナダのlinus Media Groupと米国のKIOXIAが達成し計算された300兆桁です。ギネス世界記録として公式に認定されています。この記録は、Chudnovskyとy-cruncherプログラムが使用され、SSDクラスタを活用した大規模な計算が行われました。300兆桁目は5であることが確認されています。
これだけの計算を行っても円周率πは収束をしておらず、どこかで循環しているという報告もまだなされていません。ただし、計算桁数は膨大になっても、その計算が本当に正しく計算されているのかということは、異なるアルゴリズムで計算した結果と違いがないかを検証することが重要になるのでしょう。そこで、今回はC言語編とJava言語編で行ったマチンの公式を使った円周率100万桁の計算結果が正しく行われているかをC++のプログラムを作成して検証してみます。
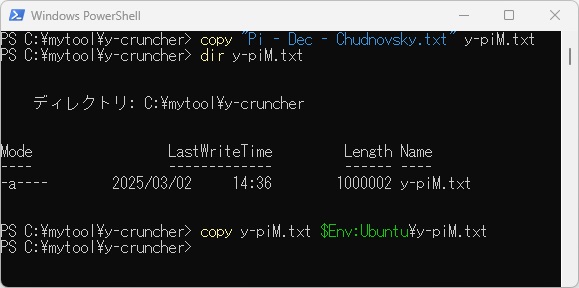
比較するのは、チェドノフスキーの公式を使って円周率を効率よく求めるソフトウェア、「y-cruncher」を使います。このソフトウェアは公開されていて、すでに数兆桁の計算まで行われています。今回はPowerShell上で以下のように「y-cruncher」で100万桁までの計算を実行しました。

計算結果が約1メガバイトの容量であることを確認し、ファイル名を「y-piM.txt」に変更し、WLS上にコピーしておきます。
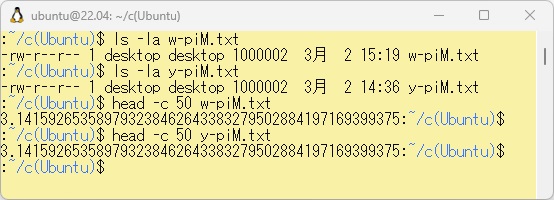
同様に、WSL上でC言語編のプログラムを利用して100万桁まで計算しますが、このままでは結果の中に「y-cruncher」の計算結果にはない、不用な空白文字や改行が入っているため、これを「trコマンド」で削除したファイルを「w-piM.txt」として以下のように作成します。

一応、二つのファイルの容量と、先頭から50バイトのデータを確認して、データの形式が同じであるかを見てみます。
これで準備が整ったので、次にプログラムをC++言語で作成します。プログラムは例題W2-5でやったようにCPUのSSEを利用して、並列処理を行い効率的に比較を行うこととします。この日本語プログラムを以下に示します。
入出力の仲間を呼ぶ
ファイル操作の仲間を呼ぶ
ベクトルの仲間を呼ぶ
#include <immintrin.h> // SSE命令セットのヘッダー(GCC)
標準的な名前空間;
#日本語定義 並列引数をセット "_mm_loadu_si128"
#日本語定義 並列に比較する "_mm_cmpeq_epi8"
#日本語定義 並列にマスクする "_mm_movemask_epi8"
#日本語定義 並列整数型にする "reinterpret_cast"
論理型 詳細に比較する( 定数指定 ベクターひな型<文字型>参照|ファイル1,
定数指定 ベクターひな型<文字型>参照|ファイル2 ) {
サイズ型 最大容量 = ファイル1の大きさ;
サイズ型 回 = 0;
// 16バイト単位で比較
反復 (; 回 + 15 < 最大容量; 回 += 16) {
整数ベクトル計算型 デ-タ列1 = 並列引数をセット(並列整数型にする( 参照|ファイル1[回] ) );
整数ベクトル計算型 デ-タ列2 = 並列引数をセット(並列整数型にする (参照|ファイル2[回] ) );
整数ベクトル計算型 比較結果 = 並列に比較する(デ-タ列1, デ-タ列2);
// マスクを作成し、不一致があれば 偽
もし ( 並列にマスクする(比較結果) != 0xffff ) ならば戻る 偽;
}
// 残りの部分を比較する
反復 ( ; 回 < 最大容量; ++回) {
もし ( ファイル1[回] != ファイル2[回] ) ならば戻る 偽;
}
戻る 真;
}
#日本語定義 バイナリモ-ド "ios::binary"
#日本語定義 位置を末尾へ "ios::ate"
#日本語定義 入力ストリーム "ifstream"
#日本語定義 の大きさ ".size()"
#日本語定義 の位置指定 ".seekg"
#日本語定義 のデータ ".data()"
#日本語定義 から読み込む ".read"
#日本語定義 のサイズを取得 ".tellg()"
論理型 ファイルを比較する( 定数指定 文字列型 参照|f1のパス,
定数指定 文字列型 参照|f2のパス ) {
入力ストリーム f1( f1のパス, バイナリモ-ド | 位置を末尾へ );
入力ストリーム f2( f2のパス, バイナリモ-ド | 位置を末尾へ );
もし ( !f1 または !f2 ) {
表示(注意)する ← "ファイルが存在しないか開けません。" ← 改行;
強制終了;
}
サイズ型 容量1 = f1のサイズを取得;
サイズ型 容量2 = f2のサイズを取得;
// サイズが違う場合は不一致
もし (容量1 != 容量2) ならば戻る 偽;
ベクターひな型<文字型> 領域1(容量1), 領域2(容量1);
f1の位置指定(0);
f2の位置指定(0);
f1から読み込む(領域1のデータ, 容量1);
f2から読み込む(領域2のデータ, 容量1);
戻る 詳細に比較する(領域1, 領域2);
}
整数型 はじまり( 整数型 入力数, 文字への番地型|入力文字列[] )
{
もし ( 入力数 != 3 ) 異常終了;
文字列型 ファイル1 = 入力文字列[1];
文字列型 ファイル2 = 入力文字列[2];
もし (ファイルを比較する(ファイル1,ファイル2)) {
表示する ← "ファイルは完全に一致しました。" ← 改行;
} それ以外 {
表示する ← "ファイルに違いが有ります。\n" ← 改行;
}
通常終了;
}
例題W2─6
#include <iostream>
#include <fstream>
#include <vector>
#include // SSE命令セットのヘッダー(GCC)
using namespace std;
bool 詳細に比較する( const vector&ファイル1,
const vector&ファイル2 ) {
size_t 最大容量 = ファイル1.size();
size_t 回 = 0;
// 16バイト単位で比較
for (; 回 + 15 < 最大容量; 回 += 16) {
__m128i デ-タ列1 = _mm_loadu_si128(reinterpret_cast( &ファイル1[回] ) );
__m128i デ-タ列2 = _mm_loadu_si128(reinterpret_cast (&ファイル2[回] ) );
__m128i 比較結果 = _mm_cmpeq_epi8(デ-タ列1, デ-タ列2);
// マスクを作成し、不一致があれば 偽
if ( _mm_movemask_epi8(比較結果) != 0xffff ) return false;
}
// 残りの部分を比較する
for ( ; 回 < 最大容量; ++回) {
if ( ファイル1[回] != ファイル2[回] ) return false;
}
return true;
}
bool ファイルを比較する( const string &f1のパス,
const string &f2のパス ) {
ifstream f1( f1のパス, ios::binary | ios::ate );
ifstream f2( f2のパス, ios::binary | ios::ate );
if ( !f1 || !f2 ) {
cerr << "ファイルが存在しないか開けません。" << endl;
exit(1);
}
size_t 容量1 = f1.tellg();
size_t 容量2 = f2.tellg();
// サイズが違う場合は不一致
if (容量1 != 容量2) return false;
vector 領域1(容量1), 領域2(容量1);
f1.seekg(0);
f2.seekg(0);
f1.read(領域1.data(), 容量1);
f2.read(領域2.data(), 容量1);
return 詳細に比較する(領域1, 領域2);
}
int main( int 入力数, char *入力文字列[] )
{
if ( 入力数 != 3 ) return 1;
string ファイル1 = 入力文字列[1];
string ファイル2 = 入力文字列[2];
if (ファイルを比較する(ファイル1,ファイル2)) {
cout << "ファイルは完全に一致しました。" << endl;
} else {
cout << "ファイルに違いが有ります。\n" << endl;
}
return 0;
}
例題W2-6を展開したもの
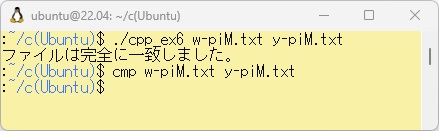
この比較プログラムは、2つのファイル名を指定して実行すると、もし違いがなければ「ファイルは完全に一致しました。」と表示します。これで100万桁の円周率計算結果は問題ないということが分かりました。また、このファイルの比較機能は、コマンド「cmp」としてWSLでも提供されています。この結果も併せて以下に示します。この「cmp」は完全に一致していれば、何もメッセージを表示しません。
最後に、「w-piM.txt」の先頭「3.1415...」を「4.1415...」と1バイトだけ変えてみたときの比較結果を以下に示します。「cmp」の方は、違いがあれば異なる行数とバイト数も表示します。
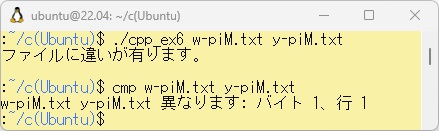
このプログラムは、PowerShell上のbcc32c V7.3ではコンパイルできませんので、bcc64 V7.7でコンパイル、リンクして任意の値を入力した実行結果を以下に示します。
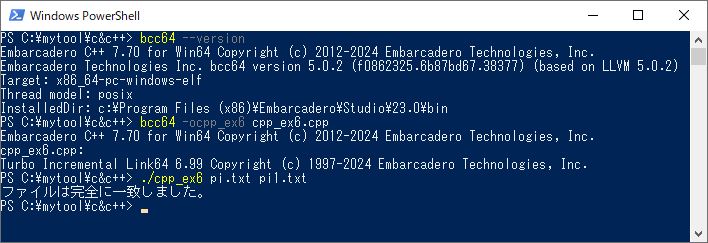
(補則)これまでC++言語編での例題はすべてCUI(コマンド・ユーザー・インターフェース)ばかりでした。Java編ではGUI(グラフィック・ユーザー・インターフェース)の例題もありますので、このC++言語編を読まれた方の中にはどうもC++言語はGUIができないのではないかと思われる方があるといけないと思い、誤解のないように一応説明します。
これまでの例題のようにコマンドプロンプト上のCUIで実行するのとは違い、RAD StudioやC++Builderというものを使うと、VCL(ビジュアル・コンポーネント・ライブラリー)というものを使うことができます。さらにRAD StudioにはマルチデバイスでGUIを開発できる環境があります。これらの機能を使えば、Windows10/11上のマウスで選択するアプリケーションなどを楽に作ることができます。
以下はVCLを使って作った「簡単なインターネットブラウザ」の例です。このようにRAD Studio/BuilderのVCLとC++言語を併用することで、Java編と同様にさまざまなGUIアプリケーションを比較的短時間で作ることが可能になります。今回は各言語で日本語を多めにということがテーマですので、このC++言語編ではやはりCUIを使った例題が主体になります。
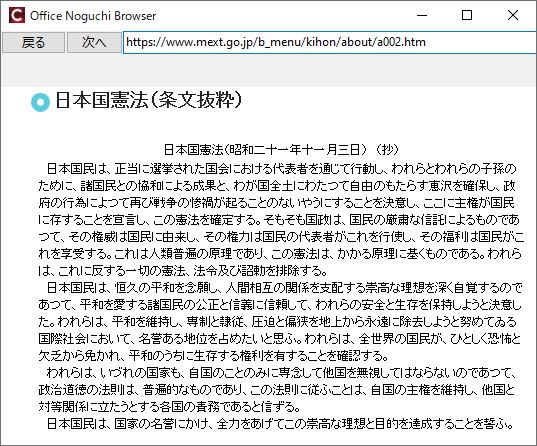
次は集合計算をやってみます。集合に関する演算は、二つの数集合の和、積、差、対称差の演算を日本語カスタマイザーを使ったC++言語でプログラムを書いてみます。
入出力の仲間を呼ぶ
集合の仲間を呼ぶ
アルゴリズムの仲間を呼ぶ
文字列の仲間を呼ぶ
反復子の仲間を呼ぶ //bcc32cのみで使用される
using namespace std;
#日本語定義 入力の最大値 "1024"
// 集合の内容を表示する
型なし 集合を表示( 定数指定 集合ひな型参照| S ) {
表示する ← "{ ";
反復 ( 整数型 数 : S ) {
表示する ← 数 ← " ";
}
表示する ← "}" ← 改行;
}
#日本語定義 に要素を追加 ".insert"
#日本語定義 状態をクリアする ".clear()"
#日本語定義 残りを無視する ".ignore"
#日本語定義 値がエラー ".fail()"
// キーボードから集合を入力する関数
集合ひな型 集合を入力(定数指定 文字列型参照| 集合名) {
集合ひな型 S;
整数型 入力値;
表示する ← 集合名 ← "の要素を数値で入力してください(非数値入力で終了):" ← 改行;
繰り返し ( 真 ) {
表示する ← "> ";
読み込む → 入力値;
もし ( !読み込む値がエラー ) {
Sに要素を追加(入力値); // 重複せずに集合に要素を追加
}
それ以外 {
読み込む状態をクリアする;
読み込む残りを無視する( 入力の最大値, '\n');
中断する;
}
}
戻る S;
}
#日本語定義 和集合の計算 "set_union"
#日本語定義 積集合の計算 "set_intersection"
#日本語定義 差集合の計算 "set_difference"
#日本語定義 対称差集合の計算 "set_symmetric_difference"
整数型 はじまり() {
// 集合の入力
集合ひな型 S1 = 集合を入力("集合1");
集合ひな型 S2 = 集合を入力("集合2");
// 入力された集合の表示
表示する ← "集合1: "; 集合を表示(S1);
表示する ← "集合2: "; 集合を表示(S2);
// 和集合の計算
集合ひな型 和集合;
和集合の計算(S1の最初, S1の最後, S2の最初, S2の最後,
入力反復子(和集合, 和集合の最初));
表示する ← "和集合: ";
集合を表示(和集合);
// 積集合の計算
集合ひな型 積集合;
積集合の計算(S1の最初, S1の最後, S2の最初, S2の最後,
入力反復子(積集合, 積集合の最初));
表示する ← "積集合: ";
集合を表示(積集合);
// 差集合 (S1 - S2) の計算
集合ひな型 差集合; 差集合の計算(S1の最初, S1の最後, S2の最初, S2の最後,
入力反復子(差集合, 差集合の最初));
表示する ← "差集合 (S1 - S2): ";
集合を表示(差集合);
// 対称差の計算
集合ひな型 対称差; 対称差集合の計算(S1の最初, S1の最後, S2の最初, S2の最後,
入力反復子(対称差, 対称差の最初));
表示する ← "対称差: ";
集合を表示(対称差);
通常終了;
}
例題W2─7
集合ひな型(set<int>)で定義された整数型コンテナは、重複しない数値要素を自動的にソートして保持します。 和集合は、2つの集合の重複しない、すべての要素の集合で、積集合は2つの集合の共通要素の集合です。 また、差集合は、最初に入力した集合の要素から次の集合の差で、対称差とは、2つの集合の両方に属さない要素の集合です。
#include <iostream>
#include <set>
#include <algorithm>
#include <string>
#include <iterator> //bcc32cのみで使用される
using namespace std;
// 集合の内容を表示する
void 集合を表示( const set<int>& S ) {
cout << "{ ";
for ( int 数 : S ) {
cout << 数 << " ";
}
cout << "}" << endl;
}
// キーボードから集合を入力する関数
set<int> 集合を入力(const string& 集合名) {
set<int> S;
int 入力値;
cout << 集合名 << "の要素を数値で入力してください(非数値入力で終了):" << endl;
while ( true ) {
cout << "> ";
cin >> 入力値;
if ( !cin.fail() ) {
S.insert(入力値); // 重複せずに集合に要素を追加
}
else {
cin.clear();
cin.ignore( 1024, '\n');
break;
}
}
return S;
}
int main() {
// 集合の入力
set<int> S1 = 集合を入力("集合1");
set<int> S2 = 集合を入力("集合2");
// 入力された集合の表示
cout << "集合1: "; 集合を表示(S1);
cout << "集合2: "; 集合を表示(S2);
// 和集合の計算
set<int> 和集合;
set_union(S1.begin(), S1.end(), S2.begin(), S2.end(),
inserter(和集合, 和集合.begin()));
cout << "和集合: ";
集合を表示(和集合);
// 積集合の計算
set<int> 積集合;
set_intersection(S1.begin(), S1.end(), S2.begin(), S2.end(),
inserter(積集合, 積集合.begin()));
cout << "積集合: ";
集合を表示(積集合);
// 差集合 (S1 - S2) の計算
set<int> 差集合; set_difference(S1.begin(), S1.end(), S2.begin(), S2.end(),
inserter(差集合, 差集合.begin()));
cout << "差集合 (S1 - S2): ";
集合を表示(差集合);
// 対称差の計算
set<int> 対称差; set_symmetric_difference(S1.begin(), S1.end(), S2.begin(), S2.end(),
inserter(対称差, 対称差.begin()));
cout << "対称差: ";
集合を表示(対称差);
return 0;
}
例題W2-7を展開したもの
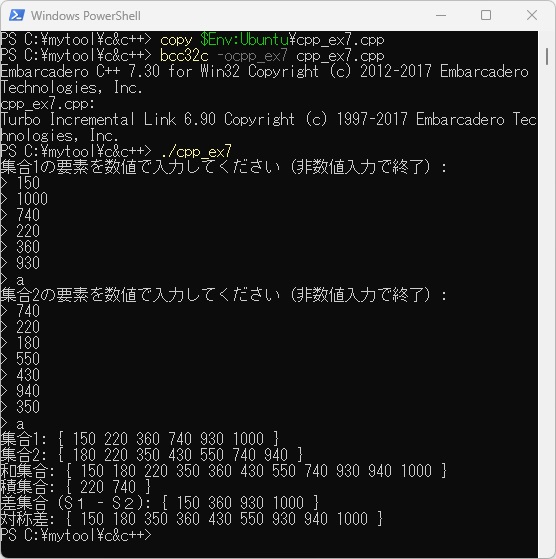
WSL上でこの例題W2-7をコンパイルし、任意の2つの集合の値を入力した実行結果を以下に示します。(入力の終了は、数値以外の文字を入力します)
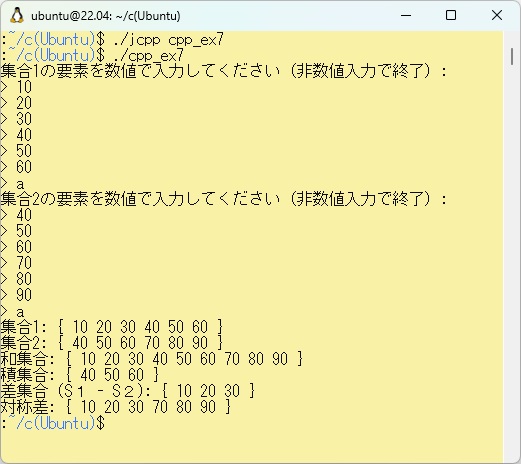
次に、PowerShell上にcpp_ex7.cppをコピーします。ここで「$Env:Ubuntu」はWSL上で、cpp_ex7.cppファイルの場所をあらかじめ設定しています。これをコンパイル、リンクして任意の2つの集合の値を入力した実行結果を以下に示します。
C言語編の「デバッグについて」という項目でも述べたように、日本語カスタマイザーを使ったC++言語でも、「filter」というFLEXを用いた簡単なツールが利用できます。日本語カスタマイザーが出力する2パス目の規則を記述してあるjcpp_rule2.lexファイルが残っていますので、この中の規則記述部分を見ることによって、日本語文字列とそれに対応する文字列がどれかということが分かります。多少手数はかかりますが、デバッグについて全く対処できないというわけではありません。
現状C++言語の仕様では、変数やクラス名など、そのまま日本語で記述することが可能になっいます。このままプログラム言語の開発環境で日本語の利用が拡大していけば幸いですが、かつて10年以上前にWindowsで利用できるclispのバージョン2.XXでは関数名などに直接日本語が利用できていたにもかかわらず、その後バージョン3.XXからは全く使えないという状況が続きました。こういうこともあるので、やはりいざというときのために日本語カスタマイザーの自動変数定義はあってしかるべきだと考えています。

今回は冒頭でも述べましたが、C++言語の豊富な機能の中でも、ほんの一部分を使って日本語化した例を示しました。 従って、スマートポインタやauto変数などを使った最近の傾向には触れていません。
また、今回はAIを一部アシスタントとして活用しました。現在AIによってプログラミングの環境が劇的に変化しています。 AIに、こういうプログラムをつくってくれと指示すると、かなり正確なコードを提示してくれたりするようになってきました。 中には指示の仕方によっては、動作しないものをありますが、今後は膨大なデータベースを持っているAIの助けを借りて、 プログラミングを考えるということが一般的になっていくのではないでしょうか。

参考サイト
各AIサイト (Grok,ChatGPT,deepseek)
GCC、GNUコンパイラコレクションのホームページ